Answers
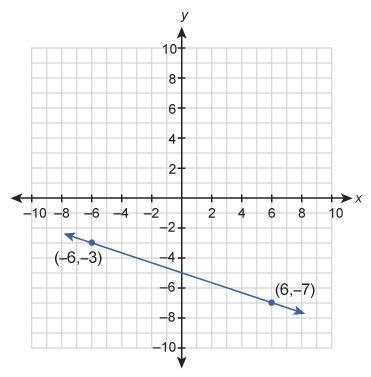
To write this equation in slope-intercept form, y = mx + b, we need to find m and b.
m, the slope, is the distance between the points' corresponding y-value divided by the distance between the points' corresponding x-value.
[tex]m=\frac{y_2-y_1}{x_2-x_1}\\m=\frac{6+6}{-7+3}\\m=\frac{12}{-4}\\m=-\frac{12}4\\m=-\frac13[/tex]
b, the y-intercept, is shown as -5, but we can solve for it as well when it is not so easy to tell the value of b. We can solve for b by substituting known solutions of x and y after we find m.
[tex]y=mx+b\\-7=-\frac136+b\\-7=-2+b\\-7+2=-2+2+b\\b=-5[/tex]
So,
[tex]y=-\frac13x-5[/tex]
Related Questions
8. Su, who is 5 feet tall, is standing at point D in the drawing. The top of her head is at point E. A tree yard is at point B with the top of the tree at point C. Su stands so her shadow meets the end of the t shadow at point A. What is the length of side BC? C С + E 5 ft А 8 ft D 24 ft A) 20 feet B 15 fut B C) 22 feet D) 18 feet
Answers
Explanation:
We would be applying similar triangles theorem.
If you check the image, there is a small triangle and a big triangle
For similar triangles, the ratio of the corresponding sides are equal.
Trianglke AEB is similar to triangle ECB
AD corresponds to AB
ED corresponds to CB
AD/AB = ED/CB
AD = 8 ft,
AB = AD + DB = 8+24 = 32
ED = 5 ft
CB = ?
Use the compound interest formula to determine the final value of the following amount. $1900 at 10.4% compounded monthly for 4.5 years . What is the final value of the amount?
Answers
Answer:
$3027.80
Explanation:
The compound interest formula is the following.
[tex]A=P(1+\frac{r}{n})^{nt}[/tex]where
A = final amount
P = principle amount
r = interest rate / 100
n = number of compounds per interval
t = time interval
Now in our case,
A = unknown
P = $1900
r = 10.4/100
n = 12 months / year ( because the interest is compounded monthly)
t = 4.5 yrs
Therefore, the compound interest formula gives
[tex]A=1900(1+\frac{10.4/100}{12})^{12*4.5}[/tex]Using a calculator, we evaluate the above to get
[tex]\boxed{A=\$3027.80}[/tex]which is our answer!
kiran ran 1/5 the length of the road which is 9 miles how many miles did he run?
Answers
Answer:0.02
Step-by-step explanation:
What is a formula for the nth term of the given sequence?135, -225,375...
Answers
Step 1: Write out the formula for a geometric sequence
[tex]\begin{gathered} T_n=ar^{n-1} \\ \text{Where} \\ T_n=\text{ the nth term} \\ a=\text{ the first term} \\ r=\text{ the common ratio} \end{gathered}[/tex]Step 2: Write out the given values and find the formula
[tex]\begin{gathered} a=135, \\ r=-\frac{225}{135}=-\frac{5}{3} \end{gathered}[/tex]Therefore the formula is given by
[tex]T_n=135(-\frac{5}{3})^{n-1}[/tex]Hence, the correct choice is the first choice
Use the law of sines Find each missing side or angle
Answers
The law of sine states that the ratio of Sine A and side a is just equal to the ratio of Sine B and side b which is also equal to the ratio of Sine C and side c. In formula, we have:
[tex]\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}[/tex]where the big letter A, B, C are the angles and the small letters are the side opposite of the angle.
In our triangle, we have angle 19 and its opposite side is "x" whereas the angle opposite of the side that has a length of 32 units is unknown.
To solve the unknown angle, we know that the total measure of the angle in a triangle is 180 degrees. Therefore, the measure of the missing angle is 180 - 19 - 26 = 135 degrees.
So, going back to the law of sine, we have:
[tex]\begin{gathered} \frac{\sin19}{x}=\frac{\sin 135}{32} \\ \text{Cross multiply.} \\ 32\sin 19=x\sin 135 \\ \text{Divide both sides by sin 135.} \\ \frac{32\sin 19}{\sin 135}=\frac{x\sin 135}{\sin 135} \\ \frac{32\sin 19}{\sin 135}=x \\ \frac{10.41818094}{0.7071067812}=x \\ 14.73\approx x \end{gathered}[/tex]Therefore, the measure of the side x is approximately 14.73 units.
To solve the length of the other side, say y, the side opposite angle 26, we can make use of the law of sine again.
[tex]\begin{gathered} \frac{\sin135}{32}=\frac{\sin 26}{y} \\ y\sin 135=32\sin 26 \\ y=\frac{32\sin 26}{\sin 135} \\ y=\frac{14.0278767}{0.7071067812} \\ y\approx19.84 \end{gathered}[/tex]The length of the other missing side opposite angle 26 is approximately 19.84 units.
Answer:
14.7
Step-by-step explanation:
yes
Plan A minutes: Plan B minutes:monday-10 monday-30tuesday-20 tuesday-40wednesday-30 wednesday-50thursday-40 thursday-60friday-50 friday-70Prove that linear functions grow by equal differences over equal intervals.
Answers
the linear function,
of plan A,
initital term a = 10
second term = 20
common difference = 20 - 10 = 10
for plan B
initial term a = 30
second term =40
the common difference = 40 - 30 = 10
thus the both linear function grow by equal difference over equal interevals.
2 Which function represents a translation of the graph of 1 = x by 8 units to the right? O A. V=(x-8) O B. v = (x+8) O c. v=872 =x2+8
Answers
Given function is,
[tex]y=x^2[/tex]For the function
[tex]y=f(x)[/tex]If we shift the graph b units to the right, the new function is
[tex]y=f(x-b)[/tex]Now, if we shift the graph of the given function 8 units to the right, the equation is
[tex]y=(x-8)^2[/tex]Hence, the correct option is (A)
your gonna need a calculator for this I don't have one help please
Answers
The correct answer is the option a) because in the table we can note that the values of the weight are strictly increasing, and the only option that meets this condition is the option a).
In a parallelogram, two adjacent sides are 2.c – 7 and 3x – 6. If the perimeter of the parallelogram is 34, find x and the shorter side of the parallelogram X= Shorter Side =
Answers
Given the information on the problem, we have the following parallelogram:
since the perimeter is 34, we can write the following equation:
[tex]2(3x-6)+2(2x-7)=34[/tex]solving for x, we get:
[tex]\begin{gathered} 2(3x-6)+2(2x-7)=34 \\ \Rightarrow6x-12+4x-14=34 \\ \Rightarrow10x-26=34 \\ \Rightarrow10x=34+26=60 \\ \Rightarrow x=\frac{60}{10}=6 \\ x=6 \end{gathered}[/tex]now that we have that x = 6, we can find the measure of the sides:
[tex]\begin{gathered} x=6 \\ 3(6)-6=18-6=12 \\ 2(6)-7=12-7=5 \end{gathered}[/tex]therefore, x = 6 and the shorter side measures 5 units
The sum of a number and -2 is no more than 6.
Answers
Answer: 8
Step-by-step explanation: if you add -2 and 8 you get 6. :) pls give me brainliest
What is the missing length? y 16 km area = 144 km y = kilometers
Answers
Area = length x width
Area = 144km^2
length = 16km
width = y
144 = 16 x y
y = 144/6 = 26 km
y = 24km
de a and perform the symmetry lest on each of the following is. eld plerd Find the in 16 r2 + 25y2 = 400 A00 (c) r2 + 4y2 = 4 (e) 4x2 + y2 = 64 (B) 9x² + 4y2 = 36 (b) 25x+6y (d) 4x + y = A () Ay? (h) 7x + y - 112 Graph the vertices, foci, endpoints of the minor axis, and endpoints of the latera recta, then draw AB is a chord of the partial ellipse with equation f(x) = ba? - x'. (a) 576x2 + 625y2 = 360,000, A (15,f(15)), B(20, f(20)) (b) 49x 2 + 625y2 = 30,625, A (15, f(15)), B(20,f(20)) – x. Find the length of AB using
Answers
The given ellipse is
[tex]576x^2+625y^2=360,000[/tex]Where A(15, f(15)), B(20, f(20)).
First, we find f(15) and f(20) by evaluating the given expression
[tex]\begin{gathered} f(15)=576(15)^2+625y^2=360,000 \\ 576\cdot225+625y^2=360,000 \\ 129,600+625y^2=360,000 \\ 625y^2=360,000-129,600 \\ 625y^2=230,400 \\ y^2=\frac{230,400}{625} \\ y^2=368.64 \\ y=\sqrt[]{368.64} \\ y=19.2 \end{gathered}[/tex]We use the same process to find f(20).
[tex]\begin{gathered} f(20)=576(20)^2+625y^2=360,000 \\ 576\cdot400+625y^2=360,000 \\ 625y^2=360,000-230,400 \\ x^2=\frac{129,600}{576} \\ x=\sqrt[]{225}=15 \\ \end{gathered}[/tex]So, the points are A(15, 19.2) and B(20, 15). To find the distance between these points, we have to use the distance formula
[tex]\begin{gathered} d_{AB}=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ d_{AB}=\sqrt[]{(20-15)^2+(15-19.2)^2} \\ d_{AB}=\sqrt[]{5^2+(-4.2)^2}=\sqrt[]{25+17.64}=\sqrt[]{42.64} \\ d_{AB}\approx6.5 \end{gathered}[/tex]Hence, the length of AB is around 6.5 units.The answer is 139 ft provided by my teacher, I need help with the work
Answers
Answer:
139 ft
Explanation:
Given below is the diagram of the situation
the tangent ratio fo 24 degrees gives
[tex]\tan 24=\frac{h}{300}[/tex]multiplying both sides by 300 gives
[tex]300\cdot\tan 24=h[/tex][tex]h=133.57ft[/tex]We have to remember here that the measuring device was 5 ft above the ground; therefore,
[tex]\text{height}=133.57+5[/tex][tex]\text{height}=138.57ft[/tex]rounding to the nearest integer gives
[tex]\text{height}=139ft[/tex]which is our answer!
Question 2 Find the missing number that makes the expression a perfect square. a. r2 x +16 b. x2 + X – 25
Answers
(a)
Given data:
The given expression is x^2 -.......x +16.
The first expression can be written as,
[tex]\begin{gathered} x^2-.\ldots..x+16=x^2-2(x)(4)+(4)^2 \\ =x^2-8x+16 \\ =(x-4)^2 \end{gathered}[/tex]Thus, the unknown value is 8.
in a class, 2/3 of the pupils are boys. If there are 15 more boys than girls, how many pupils are there in the class (use equation method)
Answers
Solution
Step 1:
Let the number of pupils = n
[tex]\begin{gathered} Number\text{ of boys = }\frac{2}{3}n \\ Number\text{ of girls = }\frac{2}{3}n\text{ - 15} \end{gathered}[/tex]Step 2:
Write an equation to find the value of n
[tex]\begin{gathered} \frac{2}{3}n\text{ + }\frac{2}{3}n\text{ - 15 = n} \\ \frac{4n}{3}\text{ - n = 15} \\ \frac{4n\text{ - 3n}}{3}\text{ = 15} \\ \frac{n}{3}\text{ = 15} \\ \text{n = 15 }\times\text{ 3} \\ \text{n = 45} \end{gathered}[/tex]Final answer
There are 45 pupils in the class.
sugar cookies require 2 cups of flour for every 2/3 cups of sugar. how much sugar for 5 cups of flour
Answers
Billy, this is the solution to the exercise:
For answering it, we will use the Direct Rule of Three, this way:
Sugar (cups) Flour (cups)
2/3 2
x 5
____________________________
x * 2 = 5 * 2/3
2x = 10/3
Dividing by 2 at both sides:
2x/2 = 10/3 / 2
x = 10/3 * 1/2
x = 10/6
x = 1 2/3 (simplifying)
We will need 1 2/3 cups of sugar for 5 cups of flour
here is some formula of understandable things. [tex] {14471}^{2852} \times 1 + 2 - {1666}^{3} \div 145663 \times \frac{5}{3} + \sqrt{86} \tan(5) + \pi0.14 = [/tex]
Answers
here is the session with equation in question
25% of what number w is 9?=25100
Answers
25 % of 36 is 9
Explanation
Step 1
the easy way to find the percentage of any number is:
[tex]\begin{gathered} y\text{ \% of x } \\ total\text{ =x*}\frac{y}{100} \end{gathered}[/tex]so
A) let
25% of what number w is 9?
let
[tex]\begin{gathered} nubmer(x)\text{ = W} \\ percentage\text{ \lparen y\rparen=25 \%} \\ total\text{ =}9 \end{gathered}[/tex]now, replace and solve for w:
[tex]\begin{gathered} y\text{ \% of x } \\ total\text{ =x*}\frac{y}{100} \\ 9=W*\frac{25}{100} \\ 9=W*0.25 \\ divide\text{ both sides by 0.25} \\ \frac{9}{0.25}=\frac{W\times0.25}{0.25} \\ 36=W \end{gathered}[/tex]therefore ,
25 % of 36 is 9
if f is defined by the function f(x)=x-4/x-2 then lim f(x) is equivalent to which of the following
Answers
Answer:
The correct answer is the third option:
[tex]\lim_{x\to4}(\sqrt{x}-2)[/tex]Explanation:
We have the function:
[tex]f(x)=\frac{x-4}{\sqrt{x}-2}[/tex]In the numerator, we have x - 4. We can rewrite it as a difference of squares, since:
[tex]\begin{gathered} x=(\sqrt{x})^2 \\ 4=2^2 \end{gathered}[/tex]Thus:
[tex]x-4=(\sqrt{x}-2)(\sqrt{x}+2)[/tex]Then, the limit:
[tex]\begin{gathered} \lim_{x\to4}(\frac{(\sqrt{x}-2)(\sqrt{x}+2)}{(\sqrt{x}-2)} \\ \end{gathered}[/tex]We can cancel out the terms, since we are taking limit, this is, numbers that infinitely close to 4, bt never 4. This way we can cancel the terms, and get:
[tex]\lim_{x\to4}(\sqrt{x}+2)[/tex]
Find the mode of each set of data.21, 12, 12, 30, 36, 34, 40, 22
Answers
The mode of a set of data is the value that appears the most number of times in the set.
So, checking this set, we have:
21: one time
12: two times
30: one time
36: one time
34: one time
40: one time
22: one time
So the mode of this set is 12.
Find the population mean or sample mean as indicated.Sample: 24, 8, 9, 5, 19
Answers
The mean of a population set can be calculated through the formula:
[tex]\bar{x}=\frac{\sum ^n_{i\mathop=1}(x_i)}{n}[/tex]in which, n is the total number of data points that are in the set
then, with the sample given the mean can be found as,
[tex]\begin{gathered} \bar{x}=\frac{24+8+9+5+19}{5} \\ \bar{x}=\frac{65}{5} \\ \bar{x}=13 \end{gathered}[/tex]Answer:
The sample mean is 13.
Given the lengths of the three sides for ∆ABC, please list the angles in order from largest to smallest.
1. AB = 15, BC = 14, AC = 10
2. AC = 20, AB = 10, BC = 15
Answers
Answer:
1. ∠B, ∠A, ∠C2. ∠C, ∠A, ∠B
Step-by-step explanation:
We know smaller side is opposite to smaller angle and the larger side is opposite to larger angle.
Considering this we have the following1. AB = 15, BC = 14, AC = 10
Put in ascending order:
AC < BC < ABSo the opposite angles are:
B < A < C----------------------------------------------------------------------
2. AC = 20, AB = 10, BC = 15
Put in ascending order:
AB < BC < ACSo the opposite angles are:
C < A < BProblem: Solve the following equations for the given variable: 1. P = 2L + 2W for W. 2. 2x + 3y = -10 for y.
Answers
EXPLANATION
Given the equations:
1. P = 2L + 2W for W. (Subtracting 2L to both sides)
P - 2L = 2l + 2W - 2l (Dividing both sides by 2)
P/2 -2L/2 = W (Simplifying and switching)
W = P/2 - L
2. 2x + 3y = -10 for y. (Subtracting 2x to both sides)
2x - 2x + 3y = -10 -2x (Simplifying)
3y = -2x - 10 (Dividing both sides by 3)
y = -2x/3 - 10/3
The Panthers and the Vikings are competing for the state basketball championship. The data shows the height in inches of the starting lineup for
each team.
Panthers: 72, 74, 71, 73, 75
Vikings: 71, 77, 76, 74, 74
Which statement is true about the data?
Answers
The average height of the Viking's starting lineup is 1.4 inches greater than the average height of the Panther's starting lineup.
The Panthers and the Vikings are competing for the state basketball championship. The data shows the height in inches of the starting lineup for each team.
The heights of the players on the Panther's team are 72, 74, 71, 73, and 75. The heights of the players on the Viking's team are 71, 77, 76, 74, and 74.
Let the average height of the Panther's starting lineup be denoted by the variable "A1".
A1 = (72 + 74 + 71 + 73 + 75)/5
A1 = 365/5
A1 = 73
So, the average height of the Panther's starting lineup is 73 inches.
Let the average height of the Viking's starting lineup be denoted by the variable "A2".
A2 = (71 + 77 + 76 + 74 + 74)/5
A2 = 372/5
A2 = 74.4
So, the average height of the Viking's starting lineup is 74.4 inches.
The difference in the average height is calculated below.
d = A2 - A1
d = 74.4 - 73
d = 1.4
Hence, the average height of the Viking's starting lineup is 1.4 inches greater than the average height of the Panther's starting lineup.
To learn more about average, visit :
https://brainly.com/question/24057012
#SPJ9
Given the card is a club, what is the probability a card drawn at random will be a(n)…12.8?13.10 or ace?
Answers
A standard deck has 52 cards, there are four suits in the deck, "clubs", "diamonds", "hearts", and "spades". There are 13 ranks in each suit.
You know that the card drawn at random is a club. This means that there are 13 possible outcomes: Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, and K.
→ You have to determine the probability of drawing an "8" given that the card is a club. There is only one 8 of clubs between the 13 cards of the suite, the probability is equal to the number of successes divided by the total number of outcomes:
[tex]P(8|Club)=\frac{1}{13}[/tex]→ You have to determine the probability of drawing a 10 or an ace, given that the card is a club. Once again, since you know that the card's suit is a club, you have to calculate the probability considering the 13 ranks that conform to the suit.
The events "drawing the 10 of clubs" and "drawing the ace of clubs" are mutually exclusive, which means that the probability of the union between both events is equal to the sum of their individual probabilities:
[tex]P((10|Club)\cup(Ace|Club))=P(10|Club)+P(Ace|Club)[/tex]There is only one 10 within the 13 ranks of the suit, the probability can be expressed as follows:
[tex]P(10|Club)=\frac{1}{13}[/tex]You can calculate the probability of drawing the Ace of Clubs using the same logic:
[tex]P(Ace|Club)=\frac{1}{13}[/tex]Now you can calculate the union between both events:
[tex]\begin{gathered} P((10|Club)\cup(Ace|Club))=P(10|Club)+P(Ace|Club) \\ P((10|Club)\cup(Ace|Club))=\frac{1}{13}+\frac{1}{13} \\ P((10|Club)\cup(Ace|Club))=\frac{2}{13} \end{gathered}[/tex]Find greatest common factor for each group,factor completely and find real roots
Answers
SOLUTION
Write out the polynomial given
The first group of the expresion is
[tex]\begin{gathered} 3x^3+4x^2 \\ \text{Then the GCE is } \\ x^2(\frac{3x^3}{x^2}+\frac{4x^2}{x^2}) \\ \text{GCE}=x^2 \end{gathered}[/tex]GCE is x²
For the second group, we have
[tex]\begin{gathered} 75x+100 \\ \text{GCE}=25(\frac{75x}{25}+\frac{100}{25}) \\ \text{GCE}=25 \end{gathered}[/tex]The GCE for the secod group is 25
To factorise completely, we have
[tex]\begin{gathered} 3x^3+4x^2+75x+100 \\ \\ x^2(\frac{3x^3}{x^2}+\frac{4x^2}{x^2})+25(\frac{75x}{25}+\frac{100}{25}) \end{gathered}[/tex]Then by simplification, we have
[tex]\begin{gathered} x^2(3x+4)+25(3x+4) \\ \text{Then, we factor completely to get} \\ (3x+4)(x^2+25) \end{gathered}[/tex]Then factors are (3x +4)(x²+ 25)
To find the real root, we equate each of the factors to zero, hence
[tex]\begin{gathered} (3x+4)(x^2+25)=0 \\ \text{Then} \\ 3x+4=0orx^2+25=0 \\ 3x=-40rx^2=-25 \\ \end{gathered}[/tex]Thus
[tex]\begin{gathered} \frac{3x}{3}=-\frac{4}{3} \\ x=-\frac{4}{3}\text{ is a real root } \\ or\text{ } \\ x^2=-25 \\ \text{take square root} \\ x=\pm_{}\sqrt[]{-25}\text{ not a real root} \end{gathered}[/tex]Therefore, since the root of -25 is a complex number,
The only real root is x = -4/3
cole is studying ceramics and he was asked to submit 5 vessels from his collection to exhibit at the fair. he has 15. vessels that he thinks are show worthy. in how many ways can the vessels be chosen
Answers
Since he has 15 vessels and needs to choose 5, we can use a combination of 15 choose 5 to calculate the number of possible ways, since the order of the vessels inside the group of 5 is not important.
The formula to calculate a combination of n choose p is:
[tex]C(n,p)=\frac{n!}{p!(n-p)!}[/tex]Then, for n = 15 and p = 5, we have:
[tex]\begin{gathered} C(15,5)=\frac{15!}{5!(15-5)!}=\frac{15!}{5!10!}=\frac{15\cdot14\cdot13\cdot12\cdot11\cdot10!}{5\cdot4\cdot3\cdot2\cdot10!} \\ =\frac{15\cdot14\cdot13\cdot12\cdot11}{5\cdot4\cdot3\cdot2}=3003 \end{gathered}[/tex]So there are 3003 ways to choose the 5 vessels.
a dime, a nickel, and a penny are each tossed one time. which table shows all the possible ways the coins could land face up, using H for heads and T for tails?
Answers
GIVEN:
We are told that an experiment consists of tossing a dime, a nickel and a penny, each of them once.
Required;
Select which table shows all the possible ways the coins could land face up, using H for heads and T for tails.
Step-by-step solution;
First we consider the entire sample space for the experiment, and that is all the possible outcomes for this experiment. This is shown below;
[tex]HHH,\text{ }HHT,\text{ }HTH,\text{ }THH,\text{ }TTH,\text{ }THT,\text{ }HTT,\text{ }TTT[/tex]The second table shows the possible outcomes whereby all coins lands face up without any outcome of landing tails up, that is TTT. Tables 1, 3 and 4 shows possibilities of having a tails for every throw in one of the outcomes (that is, TTT).
Therefore table 2 is the only set of outcomes where the coins could land face up.
ANSWER:
Table 2 (second option).
Find the measure of chord EF. Enter your numerical answer.
Answers
Notice that each chord (CD and EF) defines a segment in the circle whose arc length has the same value. Thus, the length of both chords has to be the same; then,
[tex]\begin{gathered} CD=EF \\ \Rightarrow9x-1=41-5x \\ \Rightarrow14x=42 \\ \Rightarrow x=3 \end{gathered}[/tex]Finding the length of EF,
[tex]\begin{gathered} x=3 \\ \Rightarrow EF=41-5*3=26 \end{gathered}[/tex]Therefore, the answer is 26
I have this question and I can’t figure it out
Answers
Hello!
First, let's remember about the integers numbers.
These numbers can be positive or negative (and include the number 0). The main characteristic is that these numbers don't have a decimal part.
Knowing it, we can say that are integers:
• -1,
,• 0,
,• 2,
,• -2.
In the number line, we'll have: