Answers
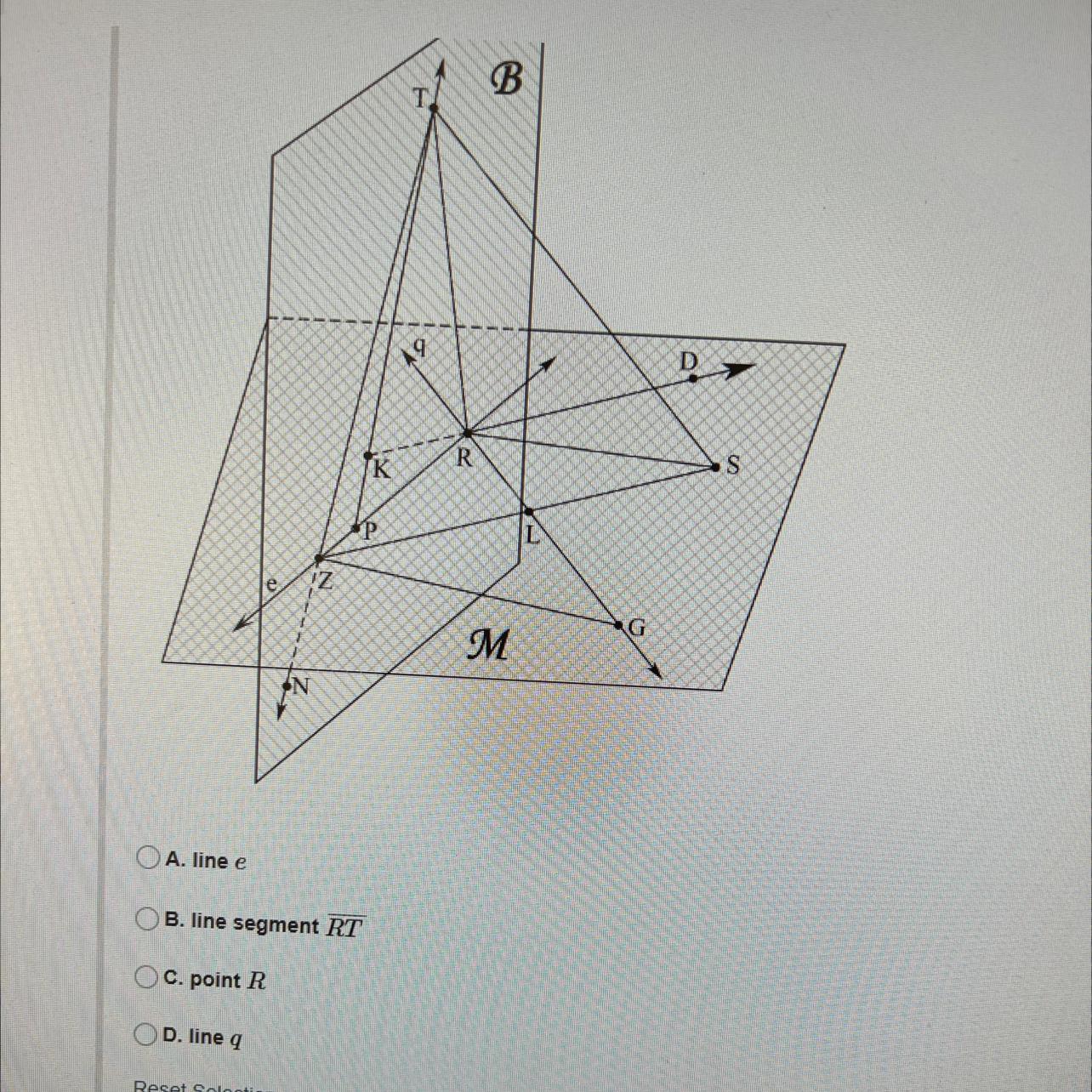
Related with the picture and your question, you should notice that an element is not contained in a set, that in your case is the plane B, when any of its points is outside of this one.
Then by the picture we could notice that the line q is not contained at the plane B, because the point G is inside q but it is not in B.
Related Questions
how much does Taryn charge to mow a lawn she mowed ,9 lawns time spent mowing lawns in an hour 7.5 and money earned $112.50
Answers
step 1
Find the unit rate
Taryn
(9,112.50)
Divide 112.50 by 9
112.50/9=$12.50 per law
Alastair
Divide 122.50 by 7
122.50/7=$17.5 per law
Find out how much Taryn earn per hour
Divide 112.50 by 7.5
112.5/7.5=$15 per hour
Find out how much Alastair earn per hour
Divide 122.50 by 5
122.5/5=$24.5 per hour
therefore
Alastair earns more per hour
the graph of each function is shown. write the function in factored format. do not include complex numbers
Answers
Notice that the graph passes through the point (-3,0), this means that the function f(x) has a root on x = -3. Then, we can use sintetic division to find the quotient of x+3 with f(x):
notice that on the last row, the last digit is 0, this means that the remainder is 0 and we can write f(x) in the following factored form:
[tex]\begin{gathered} f(x)=x^3+5x^2+12x+18= \\ (x+3)(x^2+2x+6)_{} \end{gathered}[/tex][tex]7 \sqrt{5 |4| } [/tex]3+6-4÷36×59099m
Answers
Choose whether the number given in specific notation is representing a large or small number.
Answers
Given:
[tex]\begin{gathered} a)1.2\times10^3 \\ b)7.5\times10^^{-4} \end{gathered}[/tex]To find:
The number given in a specific notation is representing a large or small number.
Explanation:
a) It can be written as,
[tex]\begin{gathered} 1.2\times10^3=1.2\times1000 \\ =1200 \end{gathered}[/tex]So, it is a large number.
b) It can be written as,
[tex]\begin{gathered} 7.5\times10^{-4}=7.5\times\frac{1}{10^4} \\ =\frac{7.5}{10000} \\ =0.00075 \end{gathered}[/tex]So, it is a small number.
Final answer:
a) Large
b) Small
rewrite csc(theta) / sec(theta) as a single trig function with no fractions
Answers
The given expression is
[tex]\frac{\csc \theta}{\sec \theta}[/tex][tex]\text{ We know that }csc\theta=\frac{1}{\sin x}\text{ and }\sec \theta=\frac{1}{cos\theta}\text{.}[/tex]Using the reciprocal, we get
[tex]\frac{\csc\theta}{\sec\theta}=\frac{\frac{1}{\sin\theta}}{\frac{1}{\cos \theta}}[/tex][tex]\text{ Use }\frac{\frac{a}{b}}{\frac{c}{d}}=\frac{a}{b}\times\frac{d}{c}[/tex][tex]\frac{\csc\theta}{\sec\theta}=\frac{1}{\sin\theta}\times\frac{\cos \theta}{1}[/tex][tex]\text{ Use }\frac{\cos\theta}{\sin\theta}=\cot \theta.[/tex][tex]\frac{\csc\theta}{\sec\theta}=\cot \theta[/tex]Hence the answer is
[tex]\cot \theta[/tex]Graph the line x= -3 on the axes shown below. Type of line: Choose one
Answers
due to the equation that represents the line is a line with no slope defined and is drawn up and down and are parallel to the y-axis.
in this case, since x=-3 it means that this value won't change along the y-axis
Reflection over the y-axis Example 2 Original Point Coordinates Image Point Coordinates A (-8,2) A B (-4,9) B C (-3,2) C'
Answers
We have to reflect the 3 points shown over the y-axis.
The simple rule for reflecting over y-axis:
• keep y coordinate same
,• negate the x coordinate
So,
(x,y) would become (-x,y)
Now, let's reflect the 3 points:
A(-8,2) would become A'(8,2)
B(-4,9) would become B'(4,9)
C(-3,2) would become C'(3,2)
Write the equation of an absolute value function that has been stretched by a factor of 2, reflected across x axis, and shifted 6 units to the right
Answers
The absolute value function is the function;
[tex]y=|x|[/tex]STEP 1: To stretch this function vertically by a factor of 2 would mean multiplying the function by 2, we have as a result;
[tex]y=2|x|[/tex]STEP 2: To reflect the function over the x-axis, this means that the entire function is multiplied by a negative sign, we have as a result;
[tex]y=-2|x|[/tex]STEP 3: To shift a function horizontally by 6 units to the right means subtracting 6 from every x- value. we have as a final result;
[tex]y=-2|x-6|[/tex]Therefore, the equation of an absolute value function that has been stretched by a factor of 2, reflected across x-axis, and shifted 6 units to the right is;
[tex]y=-2|x-6|[/tex]Hii I really need help right now I don’t understand.
Answers
The function is given as,
[tex]y=4^x[/tex]For x = -1 , the value of y is calculated as,
[tex]\begin{gathered} y=4^{-1} \\ y\text{ = }\frac{1}{4} \\ y\text{ = 0.25} \end{gathered}[/tex]For x = 0 , the value of y is calculated as,
[tex]\begin{gathered} y=4^0 \\ y\text{ = 1} \end{gathered}[/tex]For x = 1 , the value of y is calculated as,
[tex]\begin{gathered} y=4^1 \\ y\text{ = 4} \end{gathered}[/tex]For x = 2, the value of y is calculated as,
[tex]\begin{gathered} y=4^2 \\ y\text{ = 16} \end{gathered}[/tex]identify the correct trigonometry formula to use to solve for the given anglea. sin-¹(1.41)b. cos-¹(1.41)c. sin-¹(.71)d. tan-¹(.71)
Answers
The definition of arctan is opposit side by adjesent side.
[tex]\begin{gathered} \text{Angle}=tan^{-1}(\frac{Oppos\text{ side}}{\text{Adjesent side}}) \\ =\tan ^{-1}(\frac{34}{48}) \\ =\tan ^{-1}(0.71) \end{gathered}[/tex]Thus, the correct option is option d.
Bring the standard form of the equation of the line through the pair of points (5,2) and (5,-7)
Answers
The equation is
x = 5
Explanation:The equation of a line is given as:
[tex]y=mx+b[/tex]Where m is the slope and b is the y-intercept.
Given the points (5, 2) and (5, -7)
The slope is:
[tex]m=\frac{y_2-y_1}{x_2-x_1}=\frac{-7-2}{5-5}=-\frac{9}{0}=\infty[/tex]The slope is infinite, then the equation is:
[tex]x=5[/tex]square pyramid volume 225 cubic inches , base Edge 5 in . Determine the height of the pyramid
Answers
The volume of a pyramid is:
[tex]V=\frac{1}{3}\times B\times h[/tex]Where B is the area of the base and h is the height.
Since it's a square pyramid, the base has the shape of a square. So it's area is:
[tex]B=5in\times5in=25in^{2}[/tex]And we have that the volume is 225in³. We can replace these values into the formula for the volume and solve for h:
[tex]\begin{gathered} 225in^3=\frac{1}{3}\times25in^2\times h \\ \frac{3\times225in^{3}}{25in^2}=h \\ h=27in \end{gathered}[/tex]The height of the pyramid is 27 inches
Content attributionQUESTION 5.1 POINTTranslate and solve: 6 greater than b is greater than 84.Give your answer in interval notation.Provide your answer below:
Answers
6 greater than b is
[tex]=b+6[/tex]6 greater than b is greater than 84. is represented as
[tex]b+6>84[/tex]Step :Subtract 6 from both sides
[tex]\begin{gathered} b+6>84 \\ b+6-6>84-6 \\ b>78 \\ \end{gathered}[/tex]Therefore,
[tex]\begin{bmatrix}\mathrm{Solution\colon}\: & \: b>78\: \\ \: \mathrm{Interval\: Notation\colon} & \: \mleft(78,\: \infty\: \mright)\end{bmatrix}[/tex]Hence,
The interval notation is (78,∞)
Find the value of x and y if DEFG is congruent to SPQR
Answers
ANSWER
• x = 8
,• y = 10
EXPLANATION
If DEFG is congruent to SPQR, then side QR is congruent to side FG,
[tex]2x-4=12[/tex]Add 4 to both sides of the equation,
[tex]\begin{gathered} 2x-4+4=12+4 \\ 2x=16 \end{gathered}[/tex]And divide both sides by 2,
[tex]\begin{gathered} \frac{2x}{2}=\frac{16}{2} \\ x=8 \end{gathered}[/tex]For the same reason, angles F and Q are congruent,
[tex]6y+x=68[/tex]Replace x by the value we found before,
[tex]6y+8=68[/tex]Subtract 8 from both sides of the equation,
[tex]\begin{gathered} 6y+8-8=68-8 \\ 6y=60 \end{gathered}[/tex]And divide both sides by 6,
[tex]\begin{gathered} \frac{6y}{6}=\frac{60}{6} \\ y=10 \end{gathered}[/tex]Hence, the answers are x = 8 and y = 10.
Rusell runs 9/10 mile in 5 minutes. at this rate, how many miles can he run in one minute?
Answers
Answer:
in one minute, Rusell can run 9/50 mile.
[tex]\frac{9}{50}mile[/tex]Explanation:
Given that;
Rusell runs 9/10 mile in 5 minutes.
[tex]\begin{gathered} \frac{9}{10}\text{mile }\rightarrow\text{ 5 minutes} \\ \text{dividing both sides by 5;} \\ \frac{9}{10\times5}\text{mile }\rightarrow\text{ }\frac{5}{5}\text{ minutes} \\ \frac{9}{50}\text{mile }\rightarrow\text{ 1 minutes} \end{gathered}[/tex]Therefore, in one minute, Rusell can run 9/50 mile.
[tex]\frac{9}{50}mile[/tex]Simplify the result if possible assume all variables represent positive real numbers
Answers
The function [tex]log_{b} \sqrt[3]{(\frac{x^{8} }{y^{9} z^{6} })}[/tex] is simplified to be [tex]8/3log_{b}x-3log_{b}y-2log_{b}z[/tex]
How to simplify the functionThe function is simplified using the laws of logarithm
[tex]log_{b} \sqrt[3]{(\frac{x^{8} }{y^{9} z^{6} })}[/tex]
[tex]= log_{b}(\frac{x^{8} }{y^{9} z^{6} })^{1/3}[/tex]
[tex]= log_{b}(\frac{x^{8/3} }{y^{9/3} z^{6/3} })[/tex]
[tex]= log_{b}(\frac{x^{8/3} }{y^{3} z^{2} })[/tex]
Applying the quotient rule
[tex]= log_{b}x^{8/3}-log_{b}( y^{3} z^{2})[/tex]
Applying the product rule
[tex]= log_{b}x^{8/3}-(log_{b}y^{3}+log_{b}z^{2})[/tex]
expanding the parenthesis
[tex]= log_{b}x^{8/3}-log_{b}y^{3}-log_{b}z^{2}[/tex]
Applying the exponential rule
[tex]= 8/3log_{b}x-3log_{b}y-2log_{b}z[/tex]
Learn more about logarithm rules at:
https://brainly.com/question/29420555
#SPJ1
Help please I want to know how to solve this not just the answer!!
Answers
Answer:
20 overtime hours
Step-by-step explanation:
overtime starts at 40 hours anything after that would be considered overtime
If the area of square 2 is 225 units?, andthe perimeter of square 1 is 100 units, what isthe area of square 3?
Answers
Step 1. Find the length of the side of square 2.
Since square 2 has an area of:
[tex]\text{area}=225units^2[/tex]We can calculate the length of its sides (all sides in a square are equal) with the following formula that relates the area of a square "a", which the length of its side "l":
[tex]a=l^2[/tex]Solving this equation for the length "l" by taking the square root of both sides:
[tex]\sqrt[]{a}=l[/tex]Substituting the area of square 2 to find the length of the side of square 2:
[tex]\begin{gathered} \sqrt[]{225}=l \\ 15=l \end{gathered}[/tex]The length of square 2 is 15 units:
Step 2. Find the length of the side of square 1.
We are told that the perimeter of square 1 is 100 units:
[tex]p=100\text{units}[/tex]Here, "p" represents the perimeter.
Now we use the formula that relates the perimeter "p" to the length of the side of the square "l":
[tex]p=4l[/tex]And since we need to find "l" we solve that equation for "l" by dividing both sides by 4:
[tex]\frac{p}{4}=l[/tex]Substituting the value of the perimeter to find l:
[tex]\begin{gathered} \frac{100}{4}=l \\ \\ 25=l \end{gathered}[/tex]The length of the side of square 1 is 25 units:
Step 3. Find the length of the side of square 3.
Since we are asked for the area of square 3, first we need to calculate the length of its side, and we find it by using the Pythagorean Theorem in the triangle that is in the middle of the squares.
I will label the values as follows for reference:
25 is the hypotenuse of the triangle which is represented by "c"
15 is one of the legs of the triangle which is represented by "b"
and the missing length of the side of square 3 will be the second leg of the triangle "a". The following image shows this better:
The Pythagorean theorem is as follows:
[tex]a^2+b^2=c^2[/tex]Since the letter we need is a, we solve for it:
[tex]\begin{gathered} a^2=c^2-b^2 \\ a=\sqrt[]{c^2-b^2} \end{gathered}[/tex]Now, substitute the values c and b that we previously defined:
[tex]a=\sqrt[]{(25)^2-(15)^2}[/tex]Solving the operations:
[tex]a=\sqrt[]{625-225}[/tex][tex]\begin{gathered} a=\sqrt[]{400} \\ a=20 \end{gathered}[/tex]We have found the length of the side of square 3: 20 units.
Step 4. Calculate the are of square 3 using the area formula for a square:
[tex]a=l^2[/tex]Where "l" is the length of the side of the square, in this case, 20 units:
[tex]a=(20units)^2[/tex][tex]a=400units^2[/tex]Answer:
[tex]400units^2[/tex]7a) The roots of the equation 4x^2 - 7x - 1 = 0 are G and H. Evaluate G^2+ H^2B) Write the equation of a quadratic with integer coefficients whose solutions are G^2 and H^2.Pls see the pic for more detail.
Answers
Given:
[tex]4x^2-7x-1=0[/tex]Solve:
Quadratic formula:
[tex]x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}[/tex]Where,
[tex]ax^2+bx+c=0[/tex]Compaire the equation then:
[tex]\begin{gathered} ax^2+bx+c=0 \\ 4x^2-7x-1=0 \\ a=4,b=-7,c=-1 \end{gathered}[/tex]So roots of equation is:
[tex]\begin{gathered} x=\frac{-(-7)\pm\sqrt[]{(-7)^2-4(4)(-1)}}{2(4)} \\ x=\frac{7\pm\sqrt[]{49+16}}{8} \\ x=\frac{7\pm\sqrt[]{65}}{8} \end{gathered}[/tex]So value of G and H is:
[tex]\begin{gathered} G=\frac{7+\sqrt[]{65}}{8};H=\frac{7-\sqrt[]{65}}{8} \\ G=\frac{7}{8}+\frac{\sqrt[]{65}}{8};H=\frac{7}{8}-\frac{\sqrt[]{65}}{8} \end{gathered}[/tex]So:
[tex]\begin{gathered} =G^2+H^2 \\ =(\frac{7}{8}+\frac{\sqrt[]{65}}{8})^2+(\frac{7}{8}-\frac{\sqrt[]{65}}{8})^2 \\ =(\frac{7}{8})^2+(\frac{\sqrt[]{65}}{8})^2+2(\frac{7}{8})(\frac{\sqrt[]{65}}{8})+(\frac{7}{8})^2+(\frac{\sqrt[]{65}}{8})^2-2(\frac{7}{8})(\frac{\sqrt[]{65}}{8}) \\ =2(\frac{49}{64}+\frac{65}{64}) \\ =2(\frac{114}{64}) \\ =\frac{114}{32} \\ =3.5625 \end{gathered}[/tex](B)
If roots is a and b the equation is:
[tex]x^2-(a+b)x+ab=0[/tex]Then equation is:
[tex]G^2+H^2=3.5625[/tex][tex]\begin{gathered} G^2H^2=(\frac{7}{8}+\frac{\sqrt[]{65}}{8})^2(\frac{7}{8}-\frac{\sqrt[]{65}}{8})^2 \\ =(0.875+1.00778)^2(0.875-1.00778)^2 \\ =(3.54486)(0.01763) \\ =0.0624 \end{gathered}[/tex]So equation is:
[tex]x^2-3.5625x+0.0624[/tex][tex] - 15 \ \textless \ - 4x - 3[/tex]That's the Math problem
Answers
EXPLANATION
Given the inequality
-15 < -4x - 3
Adding +4x to both sides:
-15 + 4x < -4x + 4x -3
Adding +15 to both sides:
-15 + 15 + 4x < -3 + 15
Simplifying:
4x < -15 - 3
Adding like terms:
4x < -15 - 3
Dividing both sides by 4:
x < -18/4
Simplifying the fraction:
x < -4.5
The solution is x<-4.5
answer.The number of cities in a region over time is represented by the function C(=) = 2.9(1.05). The approximate number of people per city isrepresented by the function P(t) = (1.05)35 +5.Which function best describes T(*), the approximate population in the region?OA T(I) = (3.045)* + (1.05)35 +5OB. T(1) = (6.09)45+5OC. T() = 2.9(1.05)45+5OD. Т(1) = 2.9(1.05)352 +55
Answers
Given:
[tex]\begin{gathered} \text{Number of cities: }C(x)=2.9(1.05)^x \\ \\ \text{Number of people per city: P}(x)=(1.05)^{3x+5} \end{gathered}[/tex]Let's solve for T(x) which represents the approximate population in the region.
To find the approximate population in the region, apply the formula:
[tex]T(x)=C(x)\ast P(x)[/tex]Thus, we have:
[tex]T(x)=2.9(1.05)^x\ast(1.05)^{3x+5}^{}[/tex]Let's solve the equation for T(x).
Thus, we have:
[tex]\begin{gathered} T(x)=2.9((1.05)^{3x+5}(1.05)^x) \\ \\ Apply\text{ power rule:} \\ T(x)=2.9(1.05)^{3x+5+x^{}_{}} \\ \\ T(x)=2.9(1.05)^{3x+x+5} \\ \\ T(x)=2.9(1.05)^{4x+5} \end{gathered}[/tex]Therefore, the function that best describes the approximate population in the region is:
[tex]T(x)=2.9(1.05)^{4x+5}[/tex]ANSWER:
C
[tex]T(x)=2.9(1.05)^{4x+5}[/tex]A small jet can fly 889 miles in 3.5 hours with a tailwind but only 651 miles in 3.5 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.
Answers
Given:
[tex]\begin{gathered} D_{is\tan ace\text{ travelled during tail wind}}=889miles \\ T_{\text{ime taken during tail wind}}=3.5hours \\ D_{is\tan ce\text{ travelled during headwind}}=651miles \\ T_{\text{ime taken during headwind}}=3.5hours \end{gathered}[/tex]To Determine: The speed of the jet in still air and the speed of the wind
Represent the speed of the jet in still air and the speed of the wind with unknowns
[tex]\begin{gathered} T_{he\text{ sp}eed\text{ of the jet in still air}}=x \\ T_{he\text{ sp}ed\text{ of the wind}}=y \end{gathered}[/tex]Note that the speed, distance, and time is related by the formula below
[tex]S_{\text{peed}}=\frac{D_{is\tan ce}}{T_{\text{ime}}}[/tex]Calculate the speed during the tailwind and the headwind
[tex]S_{\text{peed during tail wind}}=\frac{889}{3.5}=254milesperhour[/tex][tex]S_{\text{peed during headwind}}=\frac{651}{3.5}=186milesperhour[/tex]Note that during the tailwild, the speed of the wind and the speed of the jet in still air are in the same direction. Also during the headwind, the speed of the wind and the speed of the jet in still air are in opposite direction. Therefore average speed during the tailwind and the headwind would be
[tex]\begin{gathered} equation1\colon x+y=254 \\ equation2\colon x-y=186 \end{gathered}[/tex]Combine the two equations: Add equation 1 and equation 2 to eliminate y as shown below
[tex]\begin{gathered} x+x-y+y=254+186 \\ 2x=440 \\ x=\frac{440}{2} \\ x=220\text{ miles per hour} \end{gathered}[/tex]Substitute x = 220 in equation 1
[tex]\begin{gathered} x+y=254 \\ 220+y=254 \\ y=254-220 \\ y=34\text{ miles per hour} \end{gathered}[/tex]Hence:
The speed of the jet in still air is 220 miles per hour
The speed of the wind is 34 miles per hour
15 is 20% of what numberOA 3O B. 60O C 75O D. 300
Answers
c)75
Explanation
to figure out this, we can use a rule of three
so,
let x represents the unknown value(
[tex]\begin{gathered} if \\ 15\Rightarrow20\text{ \%} \\ \text{then} \\ x\Rightarrow100\text{ \%} \end{gathered}[/tex]make the proportion and solve for x
[tex]\begin{gathered} \frac{15}{20}=\frac{x}{100} \\ \text{cross multiply} \\ 15\cdot100=20\cdot x \\ 1500=20x \\ \frac{1500}{20}=x \\ 75=x \end{gathered}[/tex]so, the answer is
C)75
I hope this helps you
Find the equation that results from completing the square into the following equation X squared -14 X +40 equals zero
Answers
Given:
The equation is
[tex]x^2-14x+40=0[/tex]Required:
Find the equation that results from completing the square into the given equation.
Explanation:
The given equation is:
[tex]x^{2}-14x+40=0[/tex]Subtract 40 on both sides.
[tex]\begin{gathered} x^2-14x+40-40=0-40 \\ x^2-14x=-40 \end{gathered}[/tex]Add 49 on both sides.
[tex]\begin{gathered} x^2-14x+49=-40+49 \\ x^2-14x+49=9 \end{gathered}[/tex]Use the following formula:
[tex]a^2-2ab+b^2=(a-b)^2[/tex][tex](x-7)^2=9[/tex]Final answer:
The second option is the correct answer.
Which describes the effect of the transformations on the graph of f(x) = x? when changed to f(x) = - = (x - 2) = 3?A)B)reflected over x-axis, stretched vertically, shifted left 2 units, and shifteddown 3 unitsreflected over x-axis, compressed vertically, shifted right 2 units, and shiftedup 3 unitsreflected over y-axis, stretched vertically, shifted left 2 units, and shifteddown 3 unitsreflected over y-axis, compressed vertically, shifted right 2 units, and shiftedup 3 units09D)
Answers
Let me start by telling you that there is a typo in the actual question (given the answers they provide for selection)
I am going to tell you the transformations that have been applied to change the function:
[tex]f(x)=x^2[/tex]into the function:
[tex]f(x)=\frac{1}{8}(x-2)^2+3[/tex]Then, these transformations consist on:
a reflection around the x axis (due to the negative sign in front),
a horizontal shift in TWO units to the right (given by the subtraction of 2 inside the parenthesis,
then a vertical compression in 1/8 (due to the factor 1/8 outside the parenthesis
and then a vertical shift of 3 units UP due to the +3 added at the end
Then, please select answer B in the list provided
I’m not sure if I’m suppose to include “x=___” in my answer or just put the answer in alone without including the variable. Please let me know which way is correct. I’m not sure if I’m writing out the problem wrong.
Answers
SOLUTION
Given the question in the inage on the question tab;
[tex](x-9)^2=2[/tex][tex]\begin{gathered} \sqrt{(x-9)^2}=\pm\sqrt{2} \\ x-9=\pm\sqrt{2} \\ x=\pm\sqrt{2}+9 \\ \therefore x=\sqrt{2}+9,\text{ -}\sqrt{2}+9 \\ \end{gathered}[/tex]Final answer:
[tex]x=\sqrt{2}+9,\text{ -}\sqrt{2}+9[/tex]Miguel and 3 of his friends went to the movies. They originally had a total of $40.00. Each boy had the same amount of money and spent $7.50 on a ticket. How much money did each boy have left after buying his ticket. Write and solve and equation.
Answers
Solution
Miguel and 3 of his friends went to the movies.
They originally had a total of $40.00.
Since each boy have the same amount, let the amount each boy have left after the ticket be m
The amount each boy have left is
[tex]4\times m=4m[/tex]Each boy spent $7.50 on a ticket, i.e
[tex]4\times7.5[/tex]The amount of money that each boy have left can be expressed as
[tex]\begin{gathered} 4m+4(7.5)=40 \\ 4(m+7.5)=40 \end{gathered}[/tex]Solving for m
[tex]\begin{gathered} 4(m+7.5)=40 \\ \text{Divide both sides by 4} \\ \frac{4(m+7.5)}{4}=\frac{40}{4} \\ m+7.5=10 \\ \text{Collect like terms} \\ m=10-7.5 \\ m=\text{ \$2.5} \end{gathered}[/tex]Hence, each boy have $2.5 left after buying his ticket.
Answer: $2.50 would be your answer!
Step-by-step explanation: $7.50 x 4 = 30
40$ - 30 = 10
10 ÷ 4 = 2.50
hope this helps! :)
40% of the students on the field trip love the museum. If there are 20 students on the field trip, how many love the museum?
Answers
well, what's 40% of 20?
[tex]\begin{array}{|c|ll} \cline{1-1} \textit{\textit{\LARGE a}\% of \textit{\LARGE b}}\\ \cline{1-1} \\ \left( \cfrac{\textit{\LARGE a}}{100} \right)\cdot \textit{\LARGE b} \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{40\% of 20}}{\left( \cfrac{40}{100} \right)20}\implies 8[/tex]
Which expression represents the area of the remainingpaper shape in square centimeters?O (x-7)(x-9)O (3x-2)(3x-8)O (3r-4)(3x +4)O (9x - 1)(x+16)
Answers
A square corner of 16 cm² is removed from a square paper with an area of 9X squared, square centimeters. which expression represents the area of the remaining paper shape in the square centimeters?
we have taht
Find out the difference
9x^2-16
apply difference of squares
9x^2-16=(3x-4)(3x+4)
answer is
(3x-4)(3x+4)
According to one study, an average payout for slots machines is 84 cents on each dollar. What is the percent return on every dollar spent in playing slots?The percent return on every dollakspent in playing slots is %.
Answers
Given that the average payout for slots machines is 84 cents on each dollar.
We know that
[tex]100\text{ cents = 1 dollar}[/tex]The cost of return for every dollar spent is 100-84=16 cents.
The percent return on every dollar spent in playing slots is
[tex]=\frac{16}{\text{one dollar}}\times100=\frac{16}{100}\times100=16\text{ \%.}[/tex]The percent return on every dollar spent in playing slots is 16%.